Линейно-оптимизированный koт
- Давай после работы коктельчики попьем?
- Не могу.
- Почему? Да давааай. Всё ты можешь.
- Нет. У меня дома кот голодный. Надо покормить.
- Ё-моё опять этот кот. Нельзя ему еды в миску навалить с запасом на 3 дня? Ну или деньги ему оставляй, пусть в макдаке ест.
- Ему не подходит еда из макдональдса.
- Ой-ой, не подходит ему. То есть проблема только в этом? А так бы он сходил?
- Ну, хватит. Не могу. =[
- …
Вот такой диалог состоялся у меня на днях. Как видите, по мнению хозяйки кота, проблема состоит в том, что еда из макдональдса ему не подходит. Так ли это?
Что коту нужно для счастья

Перед тем как ответить на вопрос нам нужно узнать, сколько и чего именно должен съедать каждый день кот, чтобы чувствовать себя сытым и счастливым. Из недр гугла добыл следующую информацию: «Ежедневный объем пищи должен составлять от 5% до 10% от веса животного». И так, сколько мы узнали. Ответ на вопрос чего именно нашел тут. На сайте дана табличка показывающая ежедневный минимум питательных веществ для сферического кота в вакууме.
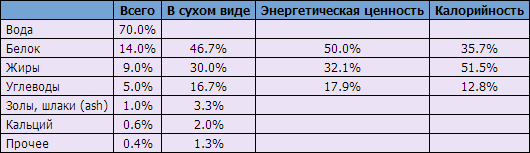
Из необходимых веществ я вычеркиваю воду которую считаю ресурсом бесконечным и бесплатным. Золу и прочее тоже не будем учитывать, пусть кот добывает их самостоятельно. Следовательно ежедневное меню в процентном отношении будет состоять из следующих веществ:

Макдональдс. Весело и вкусно
Раз уж кот должен питаться в макдональдсе, то нам пригодится этот фаил. В фаиле полная таблица продукции макдональдса с описанием содержащихся в ней веществ. Выберем любые 2 продукта. Почему два, понятно будет позже. Я выбрал гамбургеры и чикен нагетсы (в упаковках по 6 штук).

Составим мат. модель
Ежедневные потребности кота в еде запишем в виде системы неравенств:
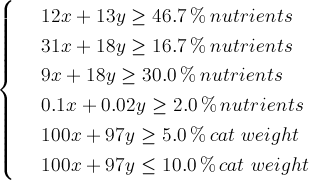
Где x,y это соответственно гамбургеры и нагетсы, а Z функция стоимости, которую будем минимизировать, чтобы кот не проел всю зарплату своей хозяйки.
Брюки превращаются
Задача превращается в классическую задачу линейного программирования или LP-задачу. Каждое неравенство из полученной системы неравенств можно представить в виде прямой разбивающей плоскость на две полуплоскости, в одной из которых все точки будут удовлетворять данному неравенству. Вот, например протеиновая полуплоскость для кота весом 1 кг:
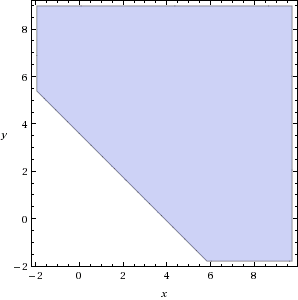
Если в виде прямых изобразить все неравенства из системы неравенств, то взаимное пересечение их полуплоскостей даст область допустимых значений переменных (ОДЗП) для целевой функции Z. А может и не даст, тогда ОДЗП будет пустым множеством. Вообще возможны такие варианты: выпуклый многогранник, выпуклая многогранная область, пустое множество.
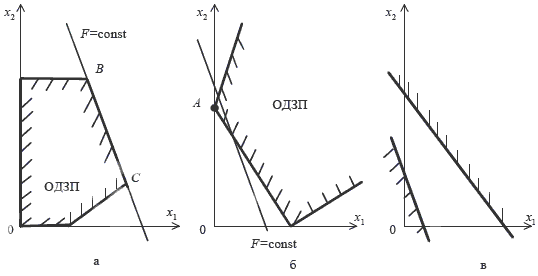
В сформулированном виде наша задача порождает пустое множество в качестве ОДЗП при любом весе кота, т.к. все зависимости линейные. Попытавшись продержаться на гамбургерах и нагетсах кот не сможет избежать переедания.
Но мы не будем сдаваться. Попробуем узнать насколько сильное переедание грозит коту, если он всё-таки попробует составить свое дневное меню из двух продуктов: гамбургеров и нагетсов. Кстати теперь должно быть ясно почему я взял только 2 продукта. При числе продуктов больше трех задача теряет наглядность и мы попадаем в n-мерное пространство с гиперплоскостями.
Hello World
Для дальнейших издевательств над животным написал на python скрипт. Откровенно говоря, весь этот пост является обоснованием для того чтобы начать писать хоть что-нибудь на языке который я решил изучать. Так что это такой своеобразный Hello World. В основе логики скрипта лежит основная теорема линейного программирования сформулированная для 2D пространства. Теорема гласит: «Целевая функция LP-задачи достигает своего экстремума в одной из вершин ОДЗП. Если целевая функция достигает экстремума в двух точках, то она достигает экстремального значения в каждой точке отрезка соединяющего эти две вершины». Наглядно это можно представить как смещение целевой функции, которая тоже является прямой в направлении своего градиента. Вот например:
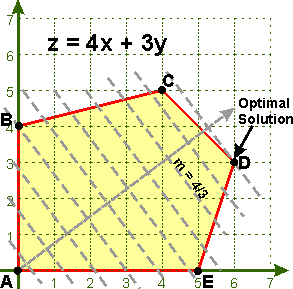
Соответственно точками экстремума для Z будут являться самые крайние точки ОДЗП. Если же целевая функция достигает экстремума (например максимума) сразу в двух точках, то она совпадет с одной из граней ОДЗП и даст бесконечное множество оптимальных решений. В скрипте используется как бы графический метод решения LP-задач, применимый только в случае 2х и 3х мерных пространств. Графический метод заключается в поиске вершин многогранника с последующей их проверкой на экстремальность. Мне же было лень в своем первом скрипте на питоне заниматься поиском вершин, поэтому я находил все точки пересечения всех прямых и пропусках их через систему неравенств как через фильтр. Если точка пересечения принадлежит ОДЗП, то может быть это вершина, а может и просто точка внутри ОДЗП, которая по основной теореме всё равно не даст экстремального результата и на итоговом ответе не скажется.
Запускаем скрипт
Пусть наш кот весит 3 кг. Сначала запустим скрипт с честными, реалистичными параметрами:
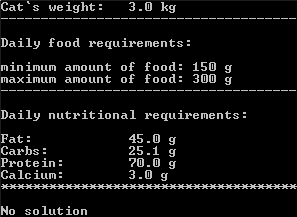
Как я уже говорил LP-задача не будет иметь решения. Чтобы поменять в параметрах оставаясь при этом более менее «честными и реалистичными»? Я начал менять максимальный объем пищи который может съесть кот в день. Повышаем значение с 10% от веса до 20%… Потом до 50%… О, черт реализмом уже и не пахнет. И наконец достигнув 100% решение найдено!
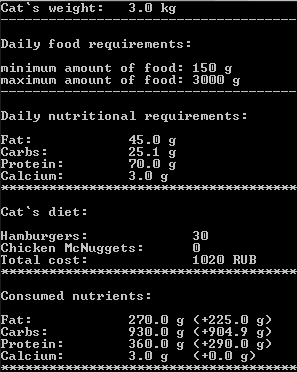
Съев всего 30 гамбургеров кот, наконец, покроет все свои потребности в питательных веществах получив при этом дикий пережор белков, жиров и углеводов. Вообще глядя на ответ мне кажется, что не только я сошел с ума, но и человек составивший таблицу полезных веществ для котов. Три грамма кальция в день! Это при том, что взрослому человеку требуется лишь 1 грамм в день. Убираем из условия задачи кальций снизив потребность в нем до пренебрежимо малого значения. И запускаем скрипт заново. Решение найдено уже при 18%.
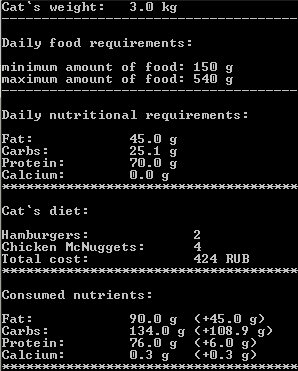
В итоге
Я успешно убил время и прозанимался ерундой весь рабочий день. Хотя не такая уж это и ерунда. Несколько десятилетий назад подобные задачи решали серьезные люди в серьезных странах. Оставайтесь с нами и вы узнаете про диету Стиглера, про пользу поп-корна и про то как готовиться к мировой войне.